判断点是否在多边形内
题目
- 要求: 编写程序判断测试用例中的四个点: p1、p2、p3、p4, 是否在同级的经纬度文件 location.json 框起来的范围内
- 测试用例
p1: 119.037089, 32.259867
p2: 118.821489, 32.077388
p3: 118.80657099, 32.0353893
p4: 118.894173, 32.077862location.json 文件
json
[
[118.897299, 32.02599],
[118.893303, 32.026212],
[118.895235, 32.028178],
[118.894384, 32.032069],
[118.892003, 32.034575],
[118.885522, 32.034631],
[118.883062, 32.035544],
[118.885012, 32.036735],
[118.885706, 32.039075],
[118.882035, 32.041],
[118.882474, 32.042578],
[118.878943, 32.041401],
[118.877634, 32.045555],
[118.879646, 32.046496],
[118.877766, 32.048919],
[118.87954, 32.049736],
[118.881587, 32.047881],
[118.887313, 32.05076],
[118.888262, 32.054747],
[118.888244, 32.058637],
[118.885969, 32.06099],
[118.88806, 32.060962],
[118.884915, 32.067108],
[118.882658, 32.067648],
[118.881499, 32.06935],
[118.875904, 32.072395],
[118.877002, 32.075343],
[118.880225, 32.072617],
[118.883879, 32.070762],
[118.881604, 32.074167],
[118.8851, 32.075523],
[118.884959, 32.078319],
[118.888051, 32.076644],
[118.888657, 32.074707],
[118.892961, 32.07461],
[118.894173, 32.077862],
[118.893066, 32.078554],
[118.897177, 32.081045],
[118.89766, 32.082457],
[118.900918, 32.082429],
[118.90834, 32.086512],
[118.907883, 32.088103],
[118.904054, 32.090663],
[118.900637, 32.095326],
[118.897124, 32.094565],
[118.891538, 32.098066],
[118.889834, 32.098315],
[118.887006, 32.101802],
[118.883589, 32.103642],
[118.878197, 32.103255],
[118.877547, 32.100847],
[118.874323, 32.09974],
[118.871741, 32.101013],
[118.868685, 32.099671],
[118.867437, 32.100709],
[118.863854, 32.100169],
[118.859963, 32.098343],
[118.858619, 32.096627],
[118.854316, 32.09772],
[118.849037, 32.096973],
[118.847851, 32.097554],
[118.84281, 32.09707],
[118.841765, 32.099035],
[118.844698, 32.098869],
[118.843029, 32.101885],
[118.834466, 32.093998],
[118.833491, 32.095063],
[118.840307, 32.101041],
[118.839569, 32.103296],
[118.842318, 32.105275],
[118.841677, 32.106036],
[118.834431, 32.104279],
[118.831392, 32.105275],
[118.826438, 32.104901],
[118.82628, 32.103601],
[118.819149, 32.10367],
[118.818033, 32.095672],
[118.811674, 32.095575],
[118.809127, 32.09617],
[118.806606, 32.098066],
[118.802461, 32.097042],
[118.799773, 32.095133],
[118.799115, 32.093237],
[118.796831, 32.091839],
[118.797788, 32.089113],
[118.793476, 32.088408],
[118.784096, 32.092268],
[118.784104, 32.041761],
[118.827167, 32.038729],
[118.826676, 32.034174],
[118.828292, 32.0338],
[118.830066, 32.039034],
[118.831655, 32.039809],
[118.838067, 32.040058],
[118.836934, 32.035752],
[118.839745, 32.034921],
[118.838076, 32.029757],
[118.843126, 32.028801],
[118.844171, 32.027804],
[118.844285, 32.022445],
[118.845981, 32.022043],
[118.846472, 32.020008],
[118.850275, 32.018845],
[118.853367, 32.020132],
[118.85327, 32.023636],
[118.857416, 32.021573],
[118.862536, 32.023567],
[118.864838, 32.021143],
[118.875105, 32.024204],
[118.876572, 32.021116],
[118.876273, 32.017446],
[118.880638, 32.014842],
[118.884959, 32.018914],
[118.895051, 32.022847],
[118.897299, 32.02599]
]思路
解题方法
射线法: 从一点向任意方向(这里取水平向右)发射一条射线, 若该射线与多边形的交点为奇数个则在多边形内部, 为偶数则在多边形外部
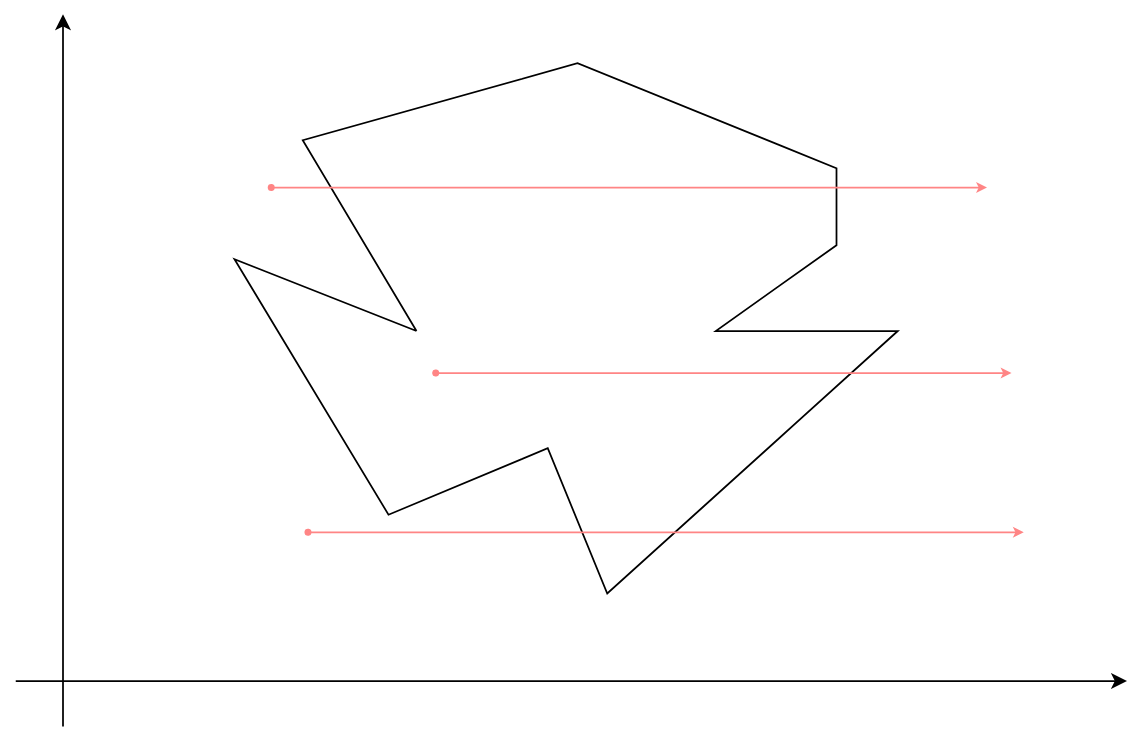
要解决的问题:
- 如何判断点与线的位置关系?
- 如何获取交点坐标?
特殊情况
- 点过一条平行边
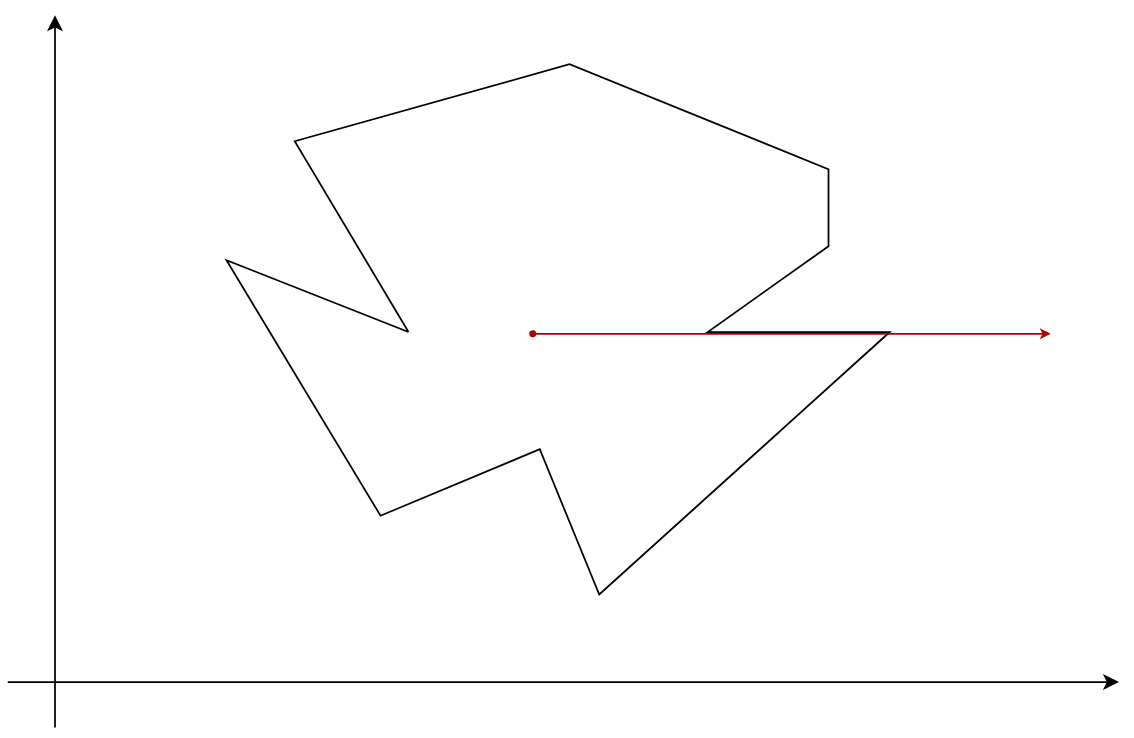
- 点过一条垂直边
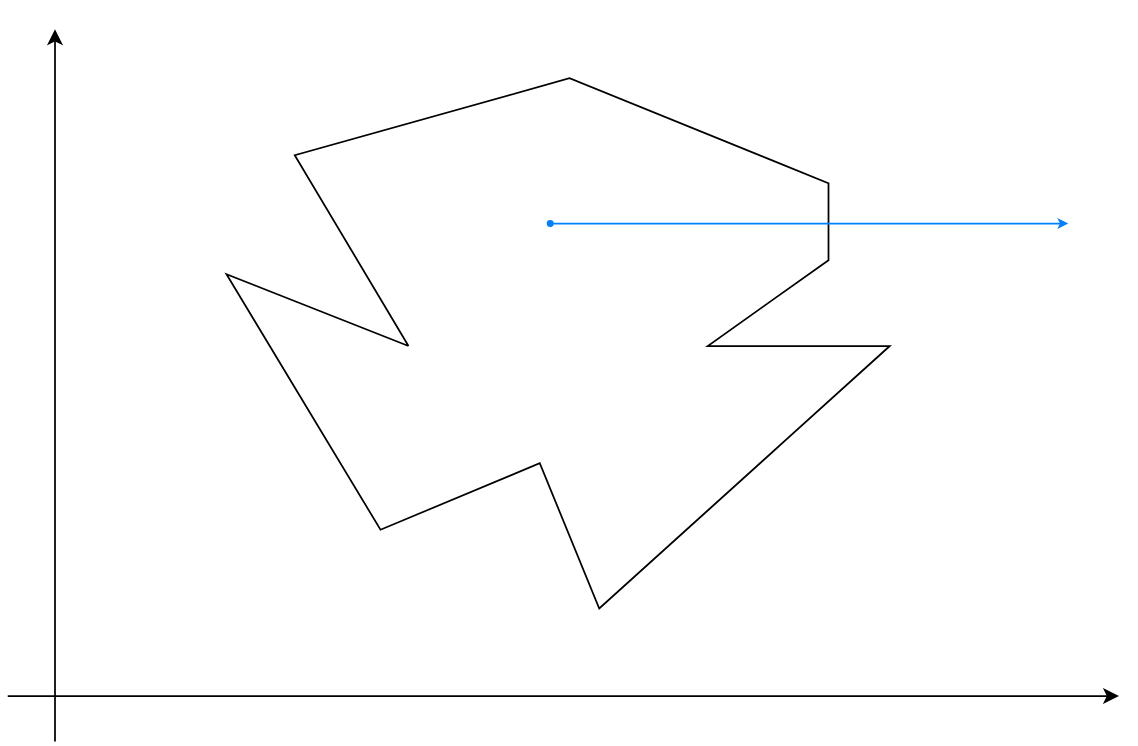
- 点过凹顶点, 凸顶点
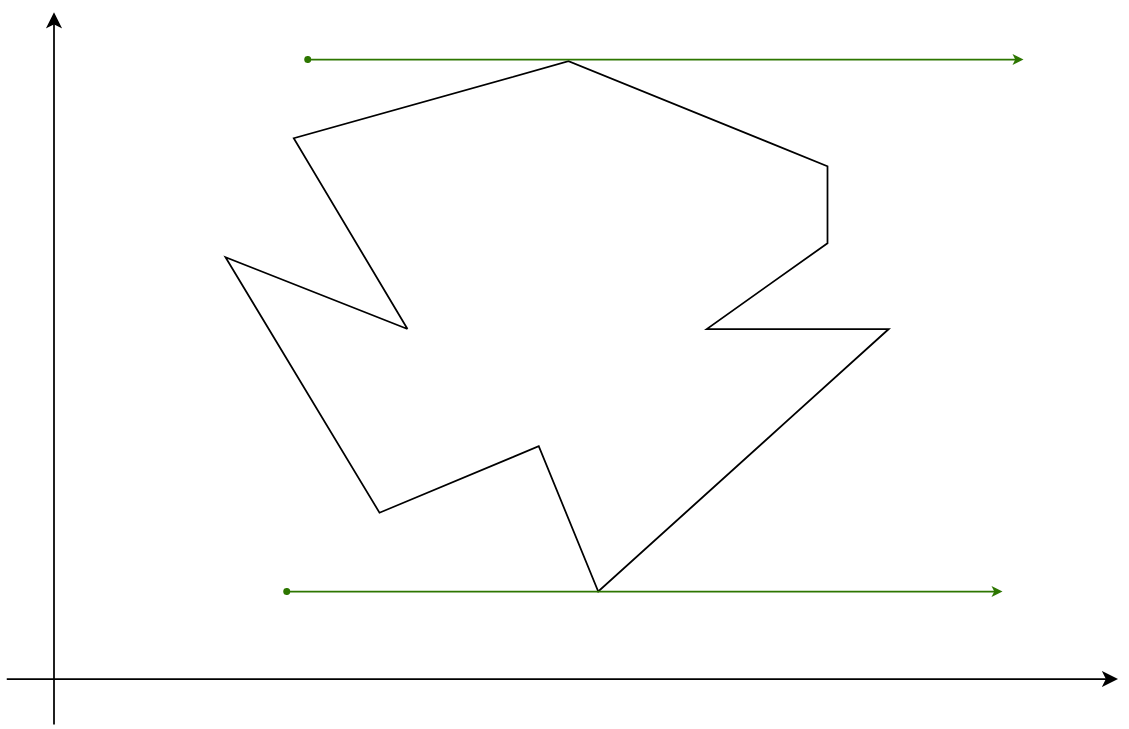
解决方案:
- 对于平行边不做考虑, 因为在相邻的线段判断中会包含顶点的判断
- 对于顶点相交的情况, 只计数所属边上的较高顶点
- 对于垂直边可直接判断相交
预备知识
若 = (, , ), = (, , );
向量的点乘和叉乘
- 点乘: = + + , 对于二维坐标 -> = ;
- 叉乘: = ( - , - , - ), 对于二维坐标 -> = - ;
向量共线判断
- 若 = , 则 和 平行
- 如果 和 共线, 则, = ||||
- = + + ;
代码
- Point.java
java
package org.pomeluce.point.model;
import java.io.Serializable;
import java.util.Objects;
/**
* @author : lucas
* @version 1.0
* @date : 2023/9/24上午10:07
* @className : Point
* @description : TODO: 点坐标
*/
public class Point implements Serializable {
private Double x;
private Double y;
public Point() {
}
public Point(Double x, Double y) {
this.x = x;
this.y = y;
}
public Double getX() {
return x;
}
public void setX(Double x) {
this.x = x;
}
public Double getY() {
return y;
}
public void setY(Double y) {
this.y = y;
}
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (!(o instanceof Point point)) return false;
if (!Objects.equals(x, point.x)) return false;
return Objects.equals(y, point.y);
}
@Override
public int hashCode() {
int result = x != null ? x.hashCode() : 0;
result = 31 * result + (y != null ? y.hashCode() : 0);
return result;
}
@Override
public String toString() {
return "Point{" +
"x=" + x +
", y=" + y +
'}';
}
}- Main.java
java
package org.pomeluce.point;
import com.fasterxml.jackson.databind.ObjectMapper;
import org.apache.commons.io.FileUtils;
import org.pomeluce.point.model.Point;
import java.io.File;
import java.io.IOException;
import java.net.URLDecoder;
import java.nio.charset.StandardCharsets;
import java.util.List;
import java.util.Objects;
/**
* @author : lucas
* @version 1.0
* @date : 2023/9/24上午10:00
* @className : Main
* @description : TODO(一句话描述该类的功能)
*/
public class Main {
public static void main(String[] args) {
// get point list file
String fileName = URLDecoder.decode(Objects.requireNonNull(Main.class.getClassLoader().getResource("latlon.json")).getPath(), StandardCharsets.UTF_8);
try {
// get json data
String sourceJson = FileUtils.readFileToString(new File(fileName), StandardCharsets.UTF_8);
// get mapper object
ObjectMapper mapper = new ObjectMapper();
// conversion string to list
@SuppressWarnings("unchecked") List<List<Double>> list = mapper.readValue(sourceJson, List.class);
/*
p1:119.037089, 32.259867 不再
p2:118.821489, 32.077388 // 内部
p3:118.80657099, 32.0353893 不再
p4:118.894173, 32.077862 线上
*/
// Point source = new Point(119.037089, 32.259867);
// Point source = new Point(118.821489, 32.077388);
Point source = new Point(118.80657099, 32.0353893);
// Point source = new Point(118.894173, 32.077862);
System.out.println(judge(list, source));
} catch (IOException e) {
throw new RuntimeException(e);
}
}
/**
* 判断点是否在点集合多边形内
*
* @param list 点集合
* @param target 目标点
* @return 返回一个 boolean 类型的判断结果
*/
public static boolean judge(List<List<Double>> list, Point target) {
// 标志变量
boolean flag = false;
for (int i = 0, j = list.size() - 1; i < list.size(); j = i++) {
// 判断点是否在边上
if (isCollinear(target, list.get(i), list.get(j))) return true;
/* 判断在多边形内 */
List<Double> p1 = list.get(i);
List<Double> p2 = list.get(j);
// 如果为水平线段则忽略
if (compareTo(p1.get(1), p2.get(1)) == 0) continue;
// 判断是否在两条边之间
if (compareTo(Math.min(p1.get(1), p2.get(1)), target.getY()) < 0 && compareTo(Math.max(p1.get(1), p2.get(1)), target.getY()) >= 0) {
// 判断该边是否为垂直竖线
if (compareTo(p1.get(0), p2.get(0)) == 0 && compareTo(target.getX(), p1.get(0)) <= 0) {
flag = !flag;
continue;
}
//
if (compareTo(target.getX(), p1.get(0) - (p1.get(0) - p2.get(0)) * (p1.get(1) - target.getY()) / (p1.get(1) - p2.get(1))) < 0) {
flag = !flag;
}
}
}
return flag;
}
/**
* 判断 target 点是否在 vec1 和 vec2 连成的线段内
*
* @param target 目标点
* @param vec1 顶点1
* @param vec2 顶点2
* @return 返回一个 boolean 类型的判断结果
*/
public static boolean isCollinear(Point target, List<Double> vec1, List<Double> vec2) {
Point p1 = vector(target, vec1);
Point p2 = vector(target, vec2);
return compareTo(cross(p1, p2), 0) == 0 && compareTo(clickMultiply(p1, p2), 0) <= 0;
}
/**
* 浮点数比较
*/
public static int compareTo(double target, double source) {
if (Math.abs(target - source) < 1e-10) return 0;
return target - source > 0 ? 1 : -1;
}
/**
* 根据点坐标获取向量
*
* @param start 起始坐标
* @param end 终点坐标
* @return 返回 Point 类型的向量结果
*/
public static Point vector(Point start, List<Double> end) {
return new Point(end.get(0) - start.getX(), end.get(1) - start.getY());
}
/**
* 向量叉乘
*
* @param start 起始向量
* @param end 终点向量
* @return 返回 double 类型的向量叉乘结果
*/
public static double cross(Point start, Point end) {
return start.getX() * end.getY() - start.getY() * end.getX();
}
/**
* 向量点乘
*
* @param start 起始向量
* @param end 终点向量
* @return 返回 double 类型的向量点乘结果
*/
public static double clickMultiply(Point start, Point end) {
return start.getX() * end.getX() + start.getY() * end.getY();
}
}